Tarihin en bilindik bilim insanlarından ve en iyi fizikçilerinden olan Albert Einstein hakkında biraz araştırma yaptıysanız Einstein'ın en bilinen denklemini de duymuşsunuzdur. Dünyayı kasıp kavuran E = mc2 denklemi, bir sistemin enerjisi (E), kütlesi (m) ve ışık hızının karesi (c2) arasındaki ilişkiyi inceliyor. Denklem son derece basit ve temel hatlarıyla anlaşılabilir olsa da anlattıkları son derece önemli.
Temel seviyede denklemi inceleyecek olursak bir nesnenin kütlesi ve içerisinde depolanan enerji arasında bir eşitlik bulunuyor. Kütle; elektrik, termal ya da kimyasal enerji gibi enerji unsurlarından yalnızca biri. Bu nedenle enerji, herhangi bir formdan diğerine dönüştürülebilir (örneğin termal enerji elektrik enerjisine dönüştürülebilir vs.).
Kütle korunmaz

Dünyada değişikliğe uğrayan ve her zaman aynı kalan şeyleri düşündüğünüz zaman kütleyi genellikle sürekli olarak sabit kalan şeyler arasına koyarız. Bir demir bloğunu alıp parçalara ayırırsanız parçaların toplamının eski bloğun kütlesine eşit olmasını beklersiniz. Kütle korunabilir olsaydı bu düşünce tamamen doğru olabilirdi.
Einstein'a göre gerçek dünyada kütle korunamaz. 26 proton, 30 nötron ve 26 elektrona sahip olan bir demir atomunu alıp bir teraziye koyarsanız kelimenin tam anlamıyla 'rahatsız edici' gerçeklerle karşılaşabilirsiniz.
Bir demir atomu, parçacıklarının ağırlıklarının ayrı ayrı toplamından daha hafiftir. Bunun yanı sıra bir demir çekirdeği 26 proton ve 30 nötronun ayrı ağırlığından daha hafiftir. Tüm bunların yanı sıra demir çekirdeklerini daha ağır bir demir çekirdeğiyle birleştirirseniz çekirdeği birleştirmek, çıkartmaktan daha fazla enerji gerektirecektir.
Yukarıda okuduğunuz tüm cümleler doğru çünkü kütle, enerjinin başka bir formu olarak karşımıza çıkıyor. Enerji istikrarı konusunda kendi yapıtaşlarından daha istikrarlı bir şey ürettiğiniz zaman üretim işlemi, sistemdeki toplam enerjiyi korumaya yetecek kadar fazla olmalı.

Bir elektronu bir atoma ya da moleküle bağlamak istediğinizde ya da bu elektronları en düşük enerji durumuna geçirmek istediğinizde bu bağlama işlemi enerji açığa çıkarır. Bu enerjinin de bir yerden gelmesi gerekir: Karmaşık ürünlerin kütleleri. Bu durum, nükleer geçiş sırasında atomik geçişlerden çok daha ciddi bir boyuta ulaşıyor. Nükleer geçişler atomik geçişlerden 1000 kat daha güçlü olabiliyor. Bu da E = mc2'den alabileceğimiz ikinci derse bir köprü niteliği taşıyor.
Enerji, yalnızca kütleleri değiştirdiğiniz zaman korunur
Dünya'yı Güneş'in etrafında dönerken hayal edin. Saniyede 30 kilometre hızla hareket eden Dünya, Güneş'ten yaklaşık 150 milyon kilometre uzakta bulunuyor. Dünyayı ve Güneş'i birbirlerinden bağımsız ve teker teker bir teraziye koyduğunuz zaman ikisinin mevcut Güneş-Dünya sisteminden daha ağır olduğunu görürsünüz.
İki nesneyi birbirine bağlayan bir çekici kuvvet olduğu zaman (bu enerji, elektronu çekirdek yörüngesinde tutan bir elektrik kuvveti, protonları ve nötronları bir arada tutan bir nükleer kuvvet ya da gezegenleri ve yıldızları tutan yerçekimsel bir kuvvet olabilir) sistemin bütünü, nesnelerin tekil ağırlıklarından daha hafiftir. Ayrıca bu nesneleri ne kadar sıkı şekilde bir araya getirirseniz bağlama işlemi o kadar enerjiyi içerisine hapseder. Bu da nihai ürünün durağan kütlesinin daha az olması anlamına gelir.
Serbest bir elektronu uzak bir mesafeden çekirdeğe bağlamak isterseniz bu durum, Güneş Sistemi'nin uzaklarında bulunan serbest bir kuyruklu yıldızı Güneş'e bağlamanıza benzer bir senaryo oluşturur. Enerjisini kaybetmezse Güneş'e yaklaşır ancak sapanla fırlatılan bir taş gibi hızla geri döner.
Sistemdeki enerjiyi azaltmanın bir ihtimali bulunabilirse nesneler daha sıkı şekilde bağlanabilir. Örneğin elektronlar çekirdeğe bağlanabilir ancak bu süreçte fotonlar açığa çıkarır. Kuyrukluyıldızlar sabit ve periyodik yörüngelere girebilir ancak bunun için başka bir gezegenin, kuyrukluyıldızın kinetik enerjisinin bir kısmını alması gerekir. Bunun yanı sıra protonlar ve nötronlar da büyük gruplar halinde birbirlerine bağlanabilir. Bu süreçte çok daha hafif bir çekirdek üretirler ve yüksek enerjili fotonları açığa çıkarırlar.
Einstein'ın E = mc2 denklemi, Güneş'in (ya da tüm yıldızların) neden parladığından sorumludur

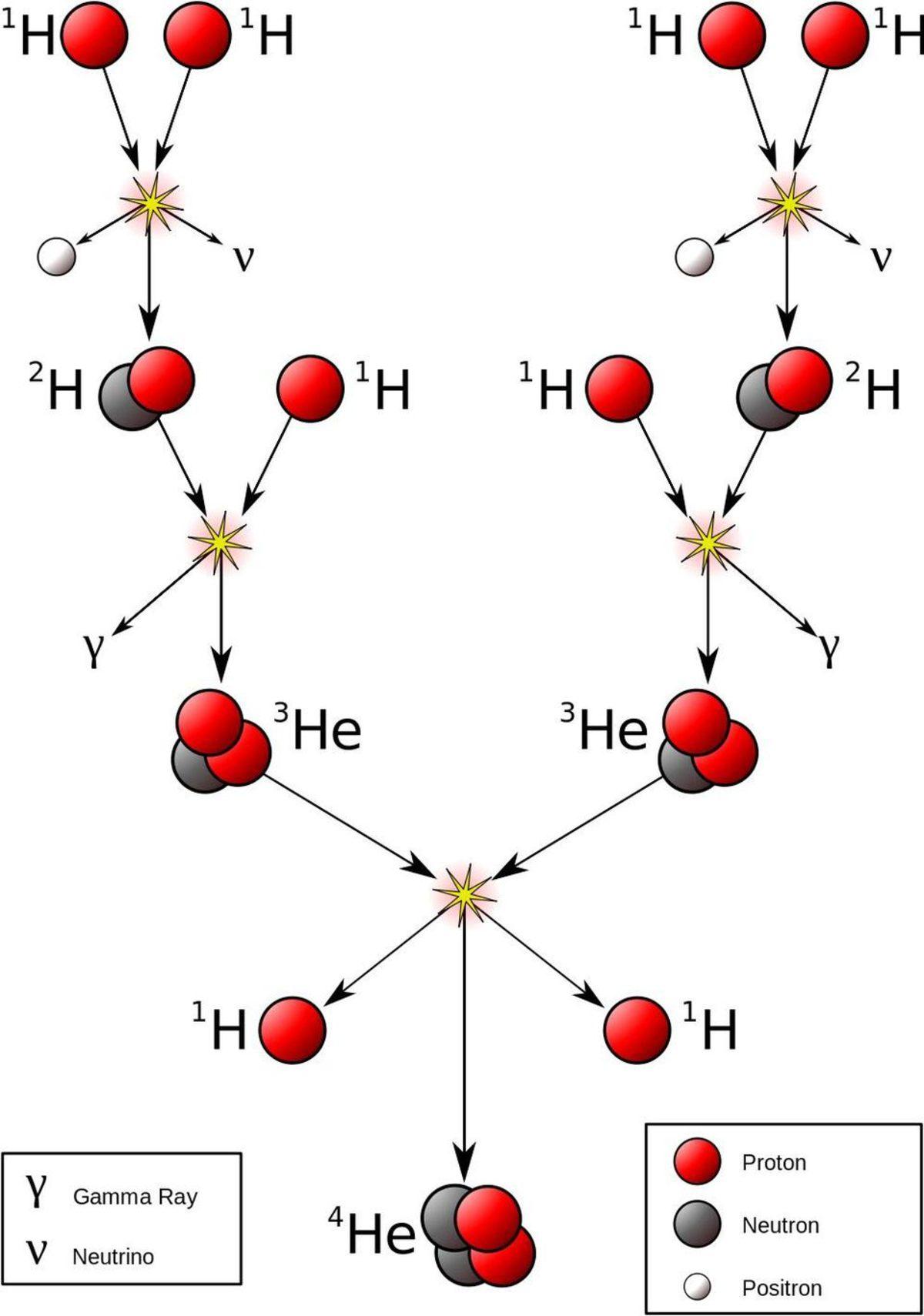
Güneş'in çekirdeği içerisinde sıcaklıklar 4 milyon Kelvin üzerine çıktığı zaman Güneş'in enerjisini sağlayan nükleer reaksiyonlar oluşur. Protonlar, bu denli uç durumlarda birleşir; enerjiyi korumak için antielektron (pozitron) ve nötrino (TÜBATerim: Sadece zayıf etkileşmelere katılan, durgun kütlesi neredeyse sıfır olan, 1/2 spinli, yüksüz temel parçacık) açığa çıkarırken bir dötron (proton ve nötronun birleşik durumu) oluşturur.
Ek protonlar ve dötronlar yeni oluşmuş parçacıkları 'bombalamaya' başlar; iki proton ve iki nötronlu helyum-4 oluşana kadar çekirdeği zincirleme reaksiyona sokar. Bu süreç yıldızlarda doğal olarak oluşur ve Güneş'in enerji kaynağı olarak bilinir.
Nihai ürün olan helyum-4'ü bir teraziye koyup helyum-4'ü oluşturan dört protonla karşılaştıracak olsaydınız nihai ürün olan helyum-4'ün %0,7 daha hafif olduğunu görürdünüz. Peki, bu nasıl oldu?
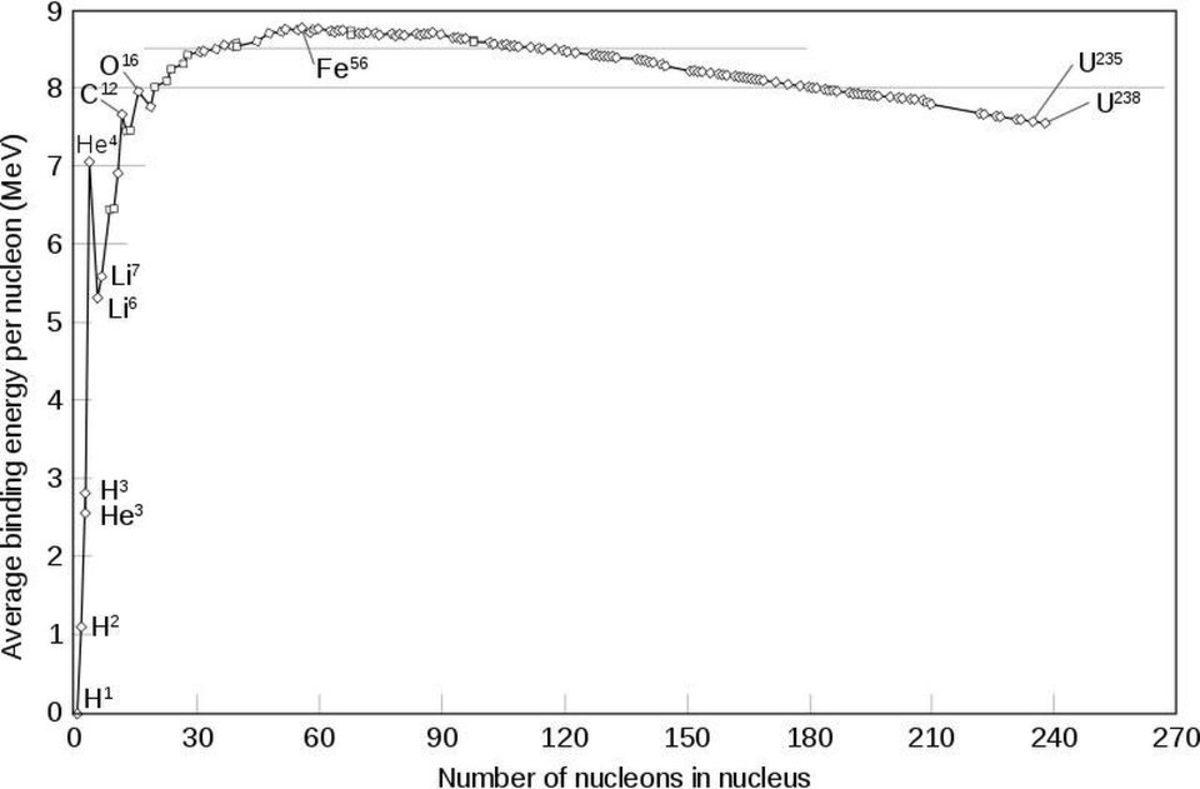
Helyum-4, ağırlığının %99,3'ünü dört protondan alır. Bu dört protonun ikisi nötrona dönüşmüş olsa da bağlayıcı kuvvet o kadar güçlüdür ki helyum-4 oluşumu sırasında 28 MeV değerinde bir enerji açığa çıkar.
Güneş, gördüğümüz enerjiyi üretebilmek için her saniye 4x1038 protonu helyum-4'e çevirir. Bu da her saniye 596 milyon ton helyum-4 üretilmesi anlamına gelir. Bu sırada 4 milyon ton kütle de E = mc2 ile saf enerjiye dönüşmüş olur. Güneş, varsayımlara göre çekirdeğinde oluşan reaksiyonlar sonucunda yaşamı boyunca Satürn kadar kütle kaybetmiştir.
Kütleyi enerjiye dönüştürmek evrendeki en verimli enerji üretimidir

%100 verimlilikten daha iyi bir yöntem var mıdır? Kesinlikle hayır. %100 verimlilik, bir reaksiyondan almayı bekleyebileceğiniz en iyi verimlilik olarak karşınıza çıkar.
E = mc2 denklemine bakacak olursanız denklem size kütleyi saf enerjiye dönüştürebileceğinizi belirtir. Bunun yanı sıra reaksiyondan ne kadar enerji alabileceğinizi de bulabilirsiniz. Dönüştürdüğünüz her 1 kilogram kütle için 9x1016 joule enerji alırsınız. Bu da 21 megaton TNT anlamına geliyor.
Bir radyoaktif fisyon ya da füzyon reaksiyonu ya da madde ve antimadde arasında bir yıkım gördüğümüz zaman reaksiyona giren ürünlerin kütleleri, nihai üründen daha fazladır. Aradaki farksa açığa çıkan enerjiye eşittir.

Açığa çıkan enerji, koşul ne olursa olsun nihai ürün ve reaksiyona giren ürünlerin kütle kaybının enerji değerine eşittir. Bu durumun en uç örneğiyse antimadde anhilasyonudur. Anhilasyon, bir atom altı parçacığını yok ederek enerjiye dönüştürme işlemine verilen isimdir. Antimadde anhilasyonu sürecinde parçacık ve antiparçacık birleşerek iki parçacıktan arda kalan enerjiye eşdeğer iki foton üretir.
Bir elektron ve pozitronu alıp anhilasyon sürecine soktuğunuz zaman her koşulda 511 keV değerinde enerjiye sahip iki adet foton elde edersiniz. Her elektron ve pozitronun durağan kütlesinin de 511 keV/c2 olması da bir rastlantı değildir. Açığa çıkan enerjiyle aynı olan değer, yalnızca (denklemde olduğu gibi) c2 ile bir araya gelmiştir. Einstein'ın en ünlü denklemi, bizlere herhangi bir parçacıkla antiparçacığın anhilasyonu sonucunda saf enerji açığa çıkabileceğini söyler.
Yalnızca ve yalnızca enerjiyi kullanarak parçacıklar üretebilirsiniz

Einstein'ın en ünlü denkleminden öğrenebileceğimiz en önemli dersler arasında birinci sırada bulunan bu kural başlangıçta tamamen saçma gelebilir. En nihayetinde iki bilardo topunu birbiriyle çarpıştırdığınız zaman yalnızca tek bir şey beklersiniz: iki adet bilardo topu.
Bu olay bilardo toplarında böyle olsa da iş parçacıklara gelince olay farklı bir boyuta ulaşabiliyor. İki elektronu alıp birbiriyle çarpıştırdığınız zaman iki adet elektron elde edersiniz ancak yeterli enerjiye sahipseniz iki elektronun yanı sıra bir madde-antimadde çiftine de sahip olabilirsiniz. Başka bir deyişle daha önce var olmayan iki adet parçacık oluşturmuş olursunuz. Bir madde (elektron, proton vb.) ve antimadde (pozitron, antiproton vb.) parçacığı.
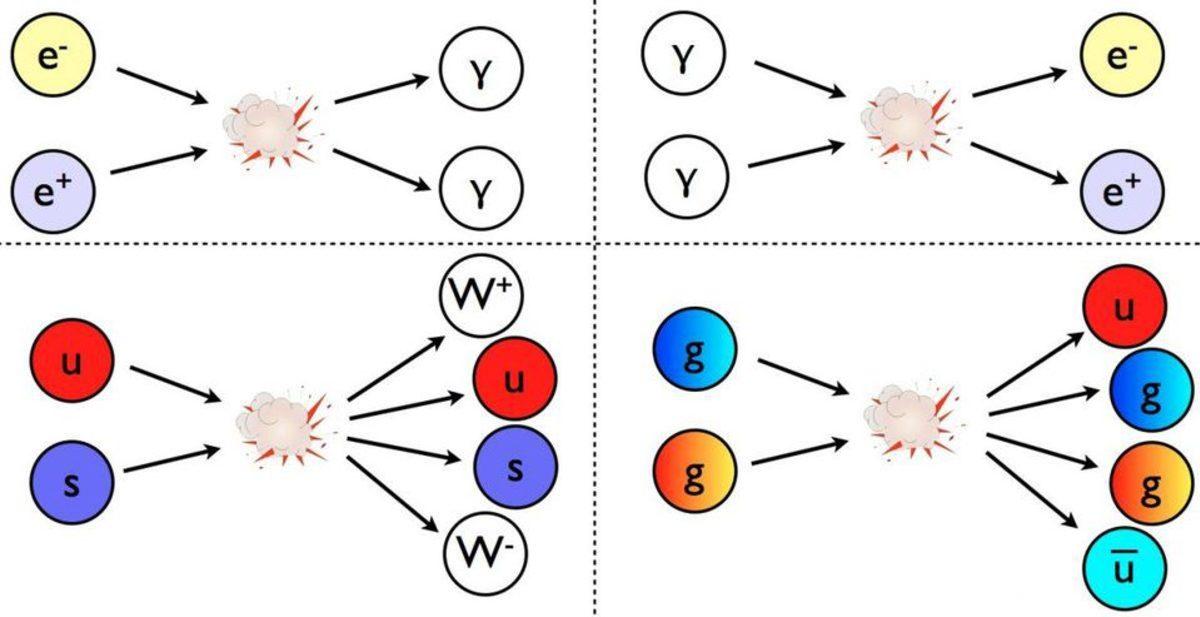
Bu işlem, madde hızlandırıcılarının nasıl yeni parçacıkları oluşturduğunu da açıklar nitelikte. Yeterli enerji sağlanması durumunda kütle (m) ile yeni parçacıklar oluşturabilirsiniz. Başka bir deyişle gereksinimleri karşılayacak kadar enerji olması durumunda m = E/c2 denklemi geçerli olacaktır. Gördüğünüz işlem de E = mc2 denkleminden türemiştir.
Einstein'ın E = mc2 denklemi, temel fiziğin yapıtaşları niteliğindedir. Kütle, yalnızca temel bir nicelik değildir ancak enerji öyledir ve kütle, enerjinin onlarca formundan biri olarak karşımıza çıkar. Kütle, önce enerjiye sonra tekrar kütleye dönüştürülebilir ve nükleer enerjiden parçacık hızlandırıcılara, atomlardan Güneş Sistemi'ne kadar her yerde karşımıza çıkar. Fizik kanunları aynı kaldığı sürece bu durum değişmeyecektir.









 Paylaş
Paylaş





 0
0








