Yazımızdaki teoremler asal sayılarla ilgili olduğu için ilk olarak asal sayılardan kısaca bahsederek başlayalım. Tanım olarak asal sayılar, kendisinden ve 1’den başka böleni bulunmayan sayılardır. Örnek olarak 7’yi verebiliriz. Kendisinden önceki 2, 3, 4 ve 5 sayılarına böldüğümüzde sürekli kesirli sonuçlar alırız. Bu özellikleri nedeniyle matematikte sayıları incelemek için asal sayılara ihtiyaç duyarız. Dilerseniz matematikçilerin çözmekte zorlandığı asal sayılarla ilgili 4 matematik problemine geçelim.
İkiz Asal
İkiz asal sayılar aralarında yalnızca 2 fark bulunan asal sayılardır. Kısaca ardışık tek sayılar da diyebiliriz. Örnek olarak 5-7, 11-13 ve 29-31 sayılarını gösterebiliriz. Ortaya atılan bir teoriye göre sonsuz sayıda ikiz asal bulunması gerekiyor. Birçok matematikçi varsayımın doğru olduğunu düşünse de, sayılar büyüdükçe asal sayılara daha az rastlanmasından ötürü kanıtlayamadı.
Bu soru yüzyıllar boyunca akılları kurcaladıktan sonra, 2013 baharında New Hampshire Üniversitesinde bir matematikçi olan Yitank Zhang tarafından yeni bir yaklaşım getirildi. Zhang'ın çalışmaları 70.000.000'den fazla ikiz asal sayının bulunmasını sağladı ve Eylül 2014'te MacArthur "Genius" bursu ile ödüllendirildi.
Goldbach'ın Düşüncesi
Basitçe ifade etmek gerekirse bu düşünceye göre 2 den büyük tüm çift rakamlar iki asal sayının toplamı şeklinde ifade edilebilir. Örneğin 4 = 2 + 2, 8 = 5 + 3, 20 = 13 + 7. Bu durum küçük çift sayılar için geçerli olsa da, henüz çok büyük sayılarda kanıtlanabilmiş değil. 21. Yüzyılda bilgisayar programlarından faydalanan araştırmacılar bu teorinin doğruluğunu 4.000.000.000.000.000.000’e kadar kanıtlamayı başardı. Bu, varsayım için oldukça iyi bir kanıt olsa da, tüm sayılar için geçerli olduğunu kanıtlamada yetersiz kalıyor.
Palindromik Asal
Matematikte tersten 99 ve 505 gibi tersten ve düzden okunuşu aynı olan sayılara palindrom denir. Ayrıca bazı sayılar hem palindrom hemde asal sayı olma özelliklerini birlikte gösterdikleri için palindromik asal adını alırlar. Palindromik asallara örnek olarak 11, 101 ve 16561 sayılarını verebiliriz. Ayrıca ortasında birçok inanışa göre hoş karşılanmayan “666” sayısını barındıran Belphegor’un asal sayısınıda örnek gösterebiliriz. “100000000000006660000000000000001” 1 ile başlayan bu sayı 13 tane sıfırla devam edip tam ortasına 666 sayısını aldıktan sonra, 13 sıfırla devam edip 1 ile kapanıyor. İkiz primlerde olduğu gibi, sonsuz sayıda Palindromik Asal olduğu düşünülse de henüz kanıtlanamadı.
Riemann Hipotezi
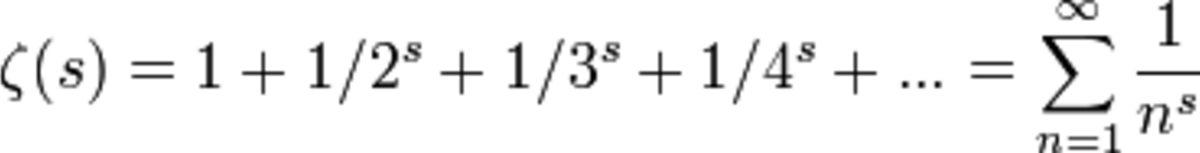
Riemann Hipotezi, matematikteki en önemli açık problemlerden biri olan Milenyum Ödül Sorunlarından biridir. Eğer biri Riemann Hipotezi’ni çözmeyi başarırsa 1 milyon dolarlık ödülün de sahibi olabilir. Bu hipotez asal sayıların belirli bir düzene sahip olduklarını ve buna göre çoğaldıklarını belirtiyor. Asal sayıların artış düzenindeki formülü bulan kişi ünün yanı sıra ekstra olarak para ödülünün de sahibi olacak.
